SPARTA

Plug-in descriptions for the SPARTA suite.

Plug-in descriptions#

All plug-ins are tested using REAPER (64-bit), which is a very affordable and flexible DAW and is the most recommended host for these plug-ins; although, other multi-channel friendly hosts (such as MaxMSP, Plogue Bidule) are also known to work. Currently, the plug-ins support sampling rates of 44.1 or 48kHz. All Ambisonics-related plug-ins conform to the Ambisonic Channel Number (ACN) ordering convention and offer support for both orthonormalised (N3D) and semi-normalised (SN3D) normalisation schemes (note that the AmbiX format refers to the combination of ACN and SN3D). The maximum transform order for these plug-ins is 10.

Hovering your mouse cursor over plugin parameters will reveal tooltips regarding the purpose of that parameter.

Thanks to the efforts of Daniel Rudrich, the relevant plug-ins also support importing and exporting loudspeaker, source, and sensors directions via .json configuration files; thus allowing for cross-compatibility between SPARTA and the IEM Ambisonics plug-in suite. More information regarding the structure of these files can be found here.

AmbiBIN#

A binaural Ambisonic decoder for headphone playback of Ambisonic signals (aka spherical harmonic or B-format signals), with a built-in rotator and head-tracking support via OSC messages. The plug-in also allows the user to import their own HRIRs via the SOFA standard. The default HRIR set is an 836-point simulation of a Kemar Dummy head, courtesy of Genelec AuralID. The plug-in offers a variety of different decoding methods, including: Least-Squares (LS), Spatial re-sampling (SPR, virtual loudspeakers), Time-Alignment (TA) [10], and Magnitude Least-Squares (MagLS) [11]. It can also impose a diffuse-coherence constraint for the current decoder, as described in [10].

This plug-in was developed by Leo McCormack, Archontis Politis, and Christoph Hold.

AmbiDEC#

A frequency-dependent Ambisonic decoder for loudspeakers. The loudspeaker directions can be user-specified for up to 64 channels, or alternatively presets for popular 2D and 3D set-ups can be selected. For headphone reproduction, the loudspeaker audio is convolved with interpolated HRTFs for each loudspeaker direction (i.e. virtual loudspeaker decoding). The plug-in also permits importing custom HRIRs via the SOFA standard.

The plug-in employs a dual decoding approach, whereby different decoder settings may be selected for the low and high frequencies, and this cross-over frequency may be dictated by the user. Several ambisonic decoders have been integrated, including the All-Round Ambisonic Decoder (AllRAD) [1] and Energy-Preserving Ambisonic Decoder (EPAD) [2]. The popular max-rE weighting/spatial-tapering [1] may also be enabled for either decoder. Furthermore, in the case of non-ideal Ambisonic signals as input (i.e. those derived from physical/simulated microphone arrays), the decoding order may be specified for the appropriate frequency ranges; where energy-preserving (EP) or amplitude-preserving (AP) normalisation is used to maintain consistent loudness between different decoding orders. This feature may also be used creatively.

Note that when the loudspeakers are uniformly distributed (e.g. a t-design), all of the included decoding approaches, except for AllRAD, become equivalent. The benefits of the Mode-Matching decoding (MMD), AllRAD and EPAD approaches may be observed for non-uniform arrangements (22.x for example).

This plug-in was developed by Leo McCormack and Archontis Politis.

AmbiDRC#

The AmbiDRC plug-in is related to this publication.

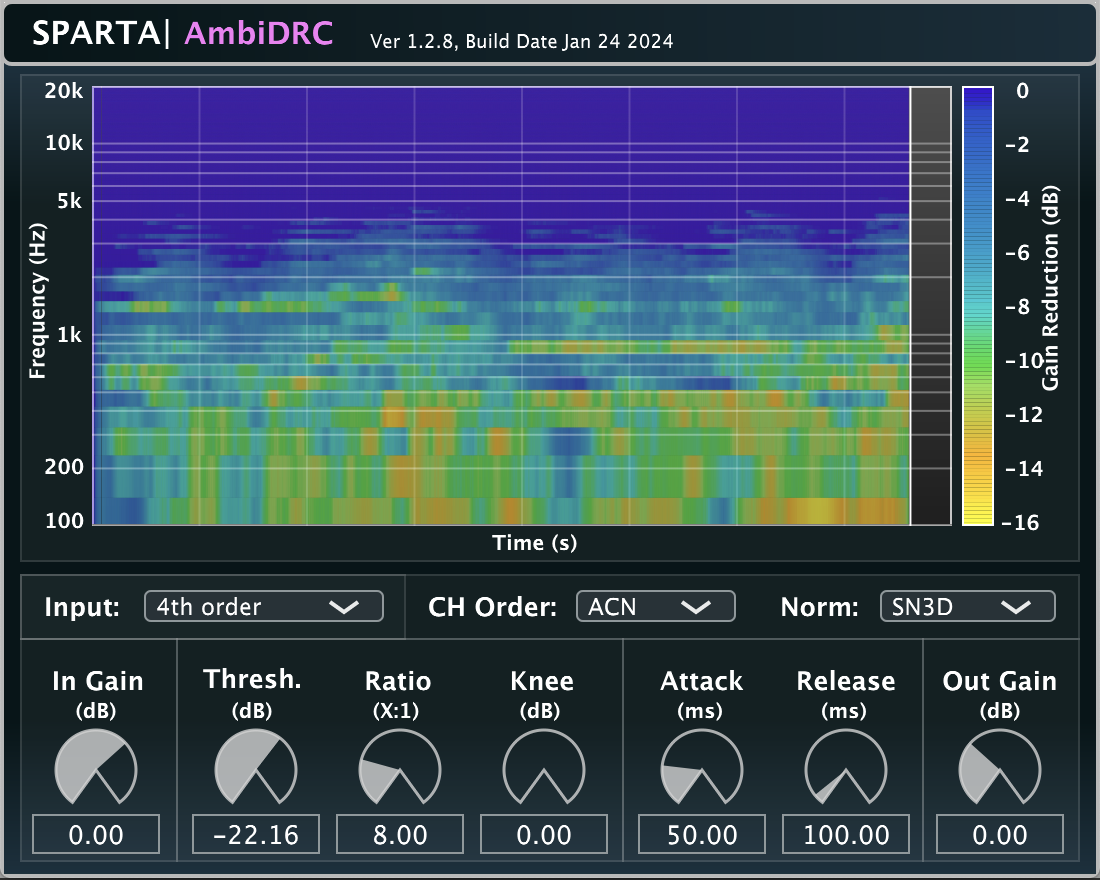
A frequency-dependent Ambisonic dynamic range compressor (DRC). The gain factors are derived by analysing the omnidirectional component for each frequency band, which are then applied also to the higher-order components. The spatial properties of the original signals remains unchanged; although, your perception of the sound scene after decoding may change. The implementation also keeps track of the frequency-dependent gain factors for the omnidirectional component over time, which is plotted on the user interface for visual feedback.

AmbiENC#

A bare-bones Ambisonic encoder which takes input signals (up to 64 channels) and encodes them into Ambisonic signals at specified directions. These Ambisonic signals describe a synthetic sound scene, where the spatial resolution of the sound scene is determined by the encoding order. Several presets have been included for convenience, which allow for 22.x etc. audio to be encoded into 1-10th order Ambisonics, for example. The panning window is also fully mouse driven, and uses an equirectangular representation of the sphere to depict the azimuth and elevation angles of each source.

AmbiRoomSim#

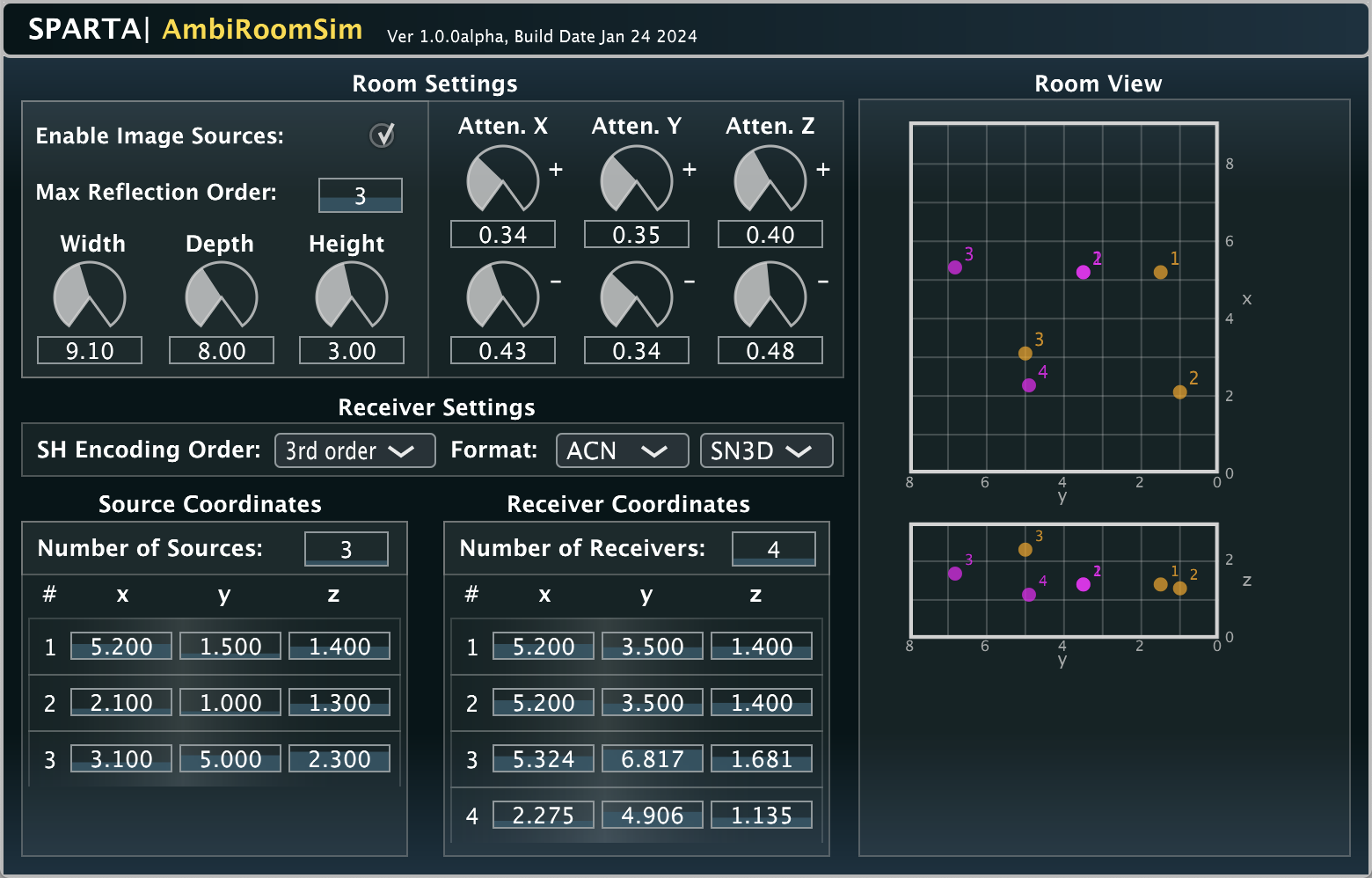
An Ambisonic encoder which includes room reflections. It is based on the image source method using a shoebox room model. It permits multiple sources, and also multiple Ambisonic receivers up to 128 channels in total; e.g. 32x first-order or 8x third-order receivers, 2x 7th-order receivers, or 1x 10th order receiver. The output receiver channels are stacked, e.g. 1-4 channels are for the 1st first-order receiver, 5-8 for the second etc.

Array2SH#

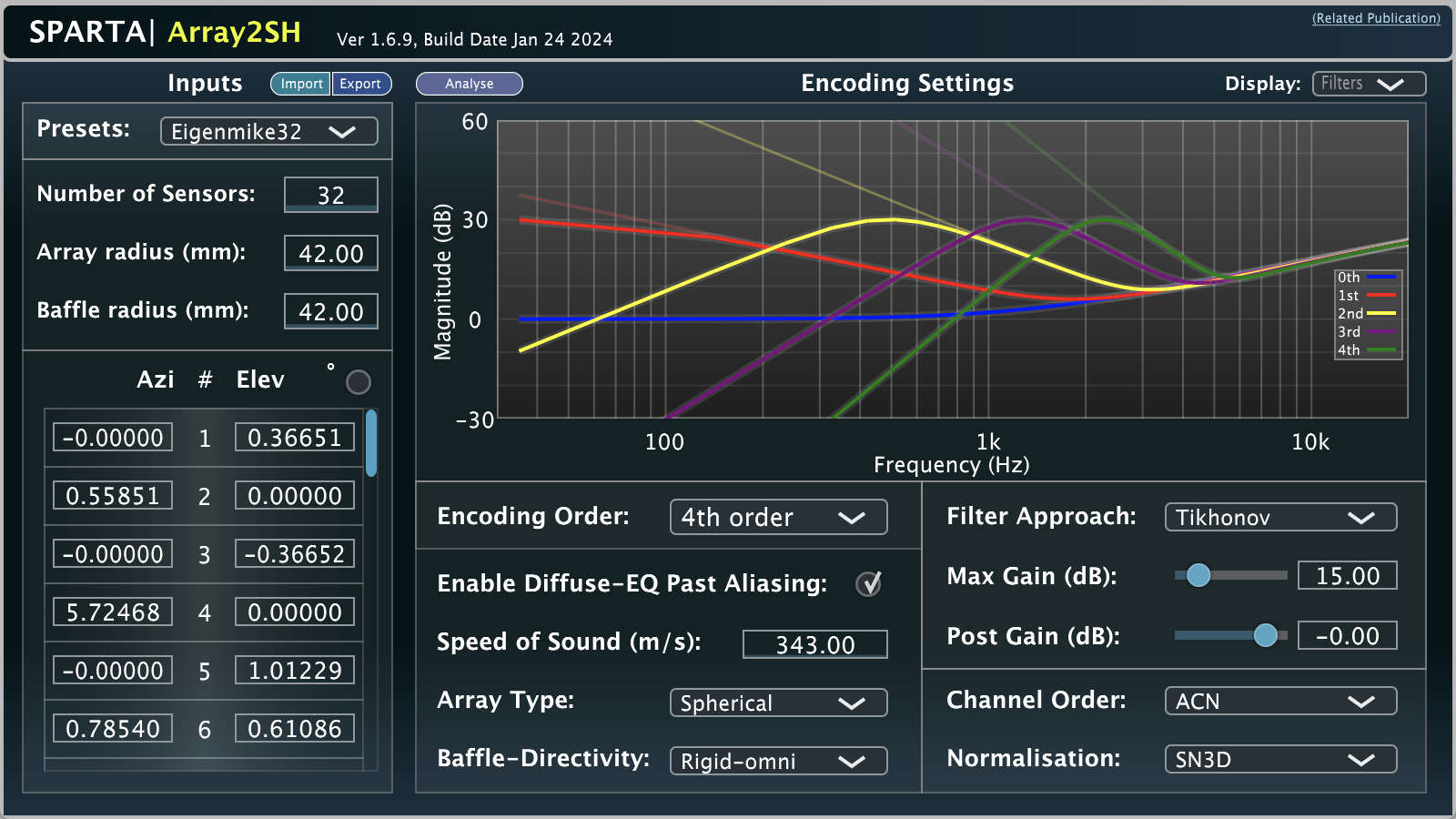
The Array2SH plug-in is related to this publication.

‘Array2SH’ spatially encodes spherical/cylindrical array signals into spherical harmonic (SH) signals, which are also referred to as Ambisonic or B-Format signals. The plug-in uses analytical descriptors, which ascertain the frequency and order-dependent influence that the physical properties of the array have on the plane-waves arriving at its surface. The plug-in allows the user to specify: the array type (spherical or cylindrical), whether the array has an open or rigid enclosure, the radius of the array, the radius of the sensors (in cases where they protrude out from the array), the sensor coordinates (up to 64 channels), sensor directivity (omni-dipole-cardioid), and the speed of sound (so that both microphone and hydrophone arrays are supported). The plug-in then determines the order-dependent equalisation curves that need to be imposed onto the initial spherical harmonic signals estimate, in order to remove the influence of the array itself. However, especially for higher-orders, this generally results in a large amplification of the low frequencies (including the sensor noise at these frequencies that accompanies it); therefore, four different regularisation approaches have been integrated into the plug-in, which allow the user to make a compromise between noise amplification and transform accuracy. These target and regularised equalisation curves are depicted on the user interface to provide visual feedback.

The plug-in also allows the user to ‘Analyse’ the spatial encoding performance using objective measures described in [7,8], namely: the spatial correlation and the level difference. Here, the encoding matrices are applied to a simulated array, which is described by multichannel transfer functions of plane waves for 812 points on the surface of the spherical/cylindrical array. The resulting encoded array responses should ideally resemble spherical harmonic functions at the grid points. The spatial correlation is then derived by comparing the patterns of these responses with the patterns of ideal spherical harmonics, where ‘1’ means they are perfect, and ‘0’ completely uncorrelated; the spatial aliasing frequency can therefore be observed for each order, as the point where the spatial correlation tends towards 0. The level difference is then the mean level difference over all directions (diffuse level difference) between the ideal and simulated components. One can observe that higher permitted amplification limits [Max Gain (dB)] will result in noisier signals; however, this will also result in a wider frequency range of useful spherical harmonic components at each order. This analysis is primarily based on code written for publication [8], which compared the performance of various regularisation approaches of encoding filters, based on both theoretical and measured array responses.

Note that this ability to balance the noise amplification with the accuracy of the spatial encoding (to better suit a given application) is very important, for example: the perceived fidelity of Ambisonic decoded audio can be rather poor if the noise amplification is set too high; therefore, typically a much lower amplification regularisation limit is used in Ambisonics reproduction when compared to sound-field visualisation algorithms, or beamformers that employ appropriate post-filtering.

For convenience, the specifications for several commercially available microphone arrays have been integrated as presets; including: mh Acoustic’s Eigenmike32/Eigenmike64, the Zylia array, and various open-tetrahedral microphone arrays. Additionally, by releasing this plug-in, one now has the ability to build/3D print their own spherical and cylindrical array, while having a convenient means of obtaining the corresponding spherical harmonic signals; for example, a four capsule open-body hydrophone array was presented in [9], which utilised this Array2SH plug-in as the first step in visualising and auralising an underwater sound scene in real-time.

This plug-in was developed by Leo McCormack, Symeon Delikaris-Manias and Archontis Politis.

Beamformer#

A simple beamforming plug-in, currently including the following static beam patterns: cardioid, hyper-cardioid, or max_rE weighted hyper-cardioid.

Binauraliser#

A plug-in which convolves input audio (up to 64 channels) with interpolated HRTFs in the time-frequency domain. The HRTFs are interpolated by applying amplitude-normalised VBAP gains [4] to the HRTF magnitude responses and the estimated inter-aural time differences (ITDs) individually, before being re-combined. The plug-in also allows the user to specify an external SOFA file for the convolution. The directions for up to 64 channels can be independently controlled. However, presets for popular 2D and 3D formats are included for convenience. Head-tracking is also supported via OSC messages in the same manner as with the Rotator plug-in.

This plug-in was developed by Leo McCormack and Archontis Politis.

BinauraliserNF#

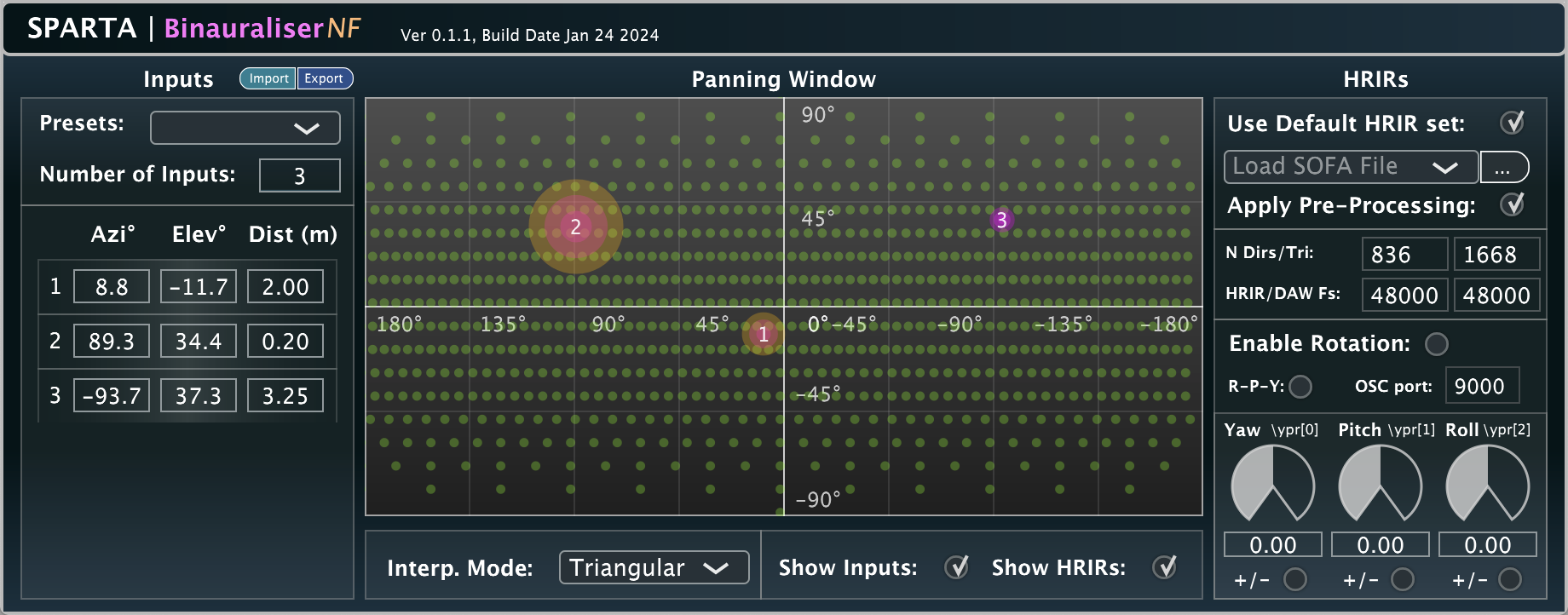
This plug-in mirrors has the functionality of the Binauraliser, with the addition of proximity filtering which reproduces the binaural effects of nearby sound sources. The implementation follows a shelving filter scheme as described in [15].

This plug-in was developed by Michael McCrea, Leo McCormack, and Sebastian Schlecht.

Decorrelator#

A simple multi-channel signal decorrelator (up to 64 channels) based on randomised time-frequency delays and cascaded all-pass filters.

DirASS#

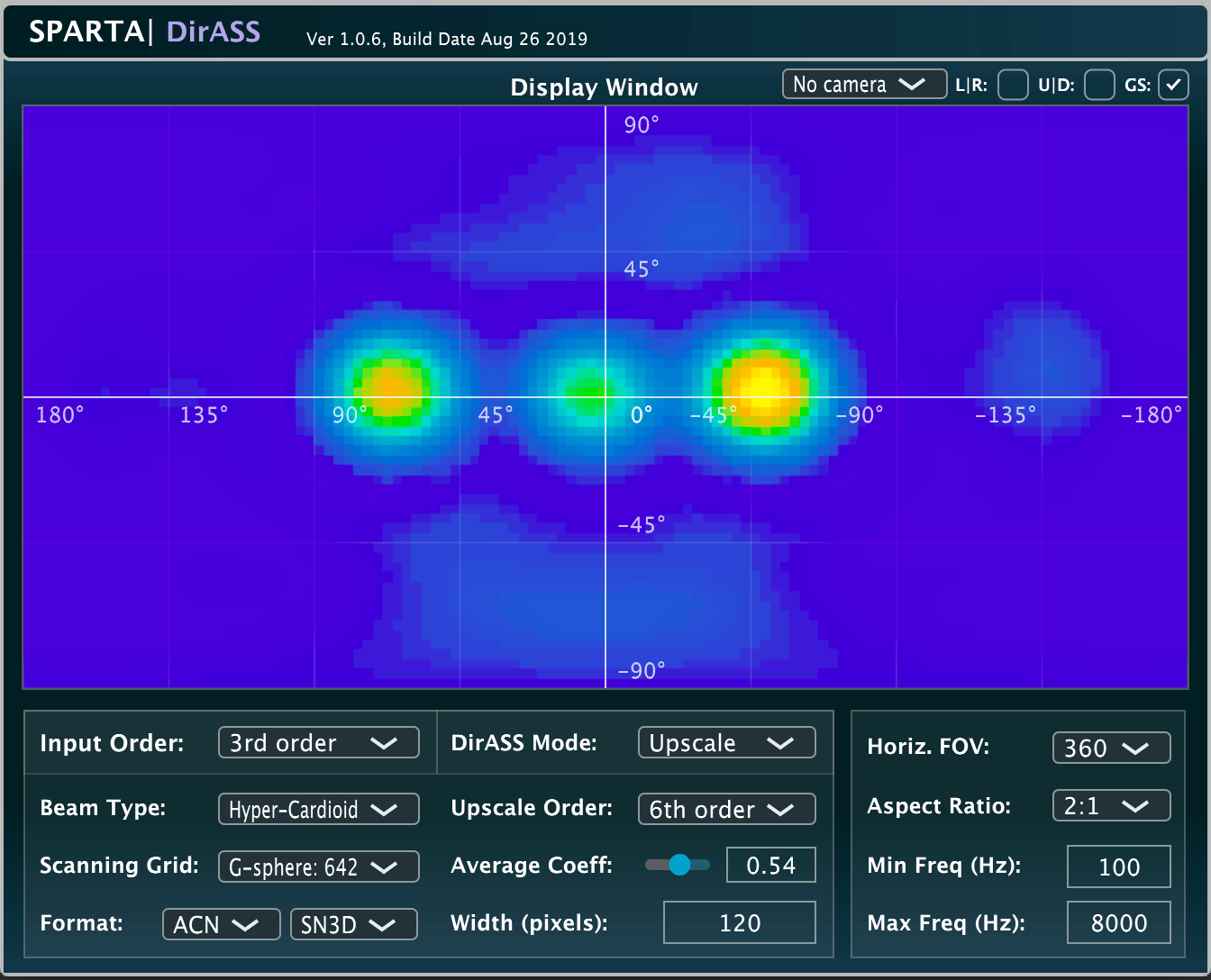
The DirASS plug-in is related to these publications: Link1, Link2.

A sound-field visualiser, which is based on the directional re-assignment of beamformer energy. This energy re-assignment is based on local DoA estimates for each scanning direction, and may be quantised to the nearest direction or upscaled to a higher-order than the input (resulting in sharper activity-maps). For example, a second-order input may be displayed with (up to) 20th order output resolution. The plug-in also allows the user to place real-time video footage behind the activity-map, in order to create a make-shift acoustic camera.

This plug-in was developed by Leo McCormack and Archontis Politis.

MatrixConv#

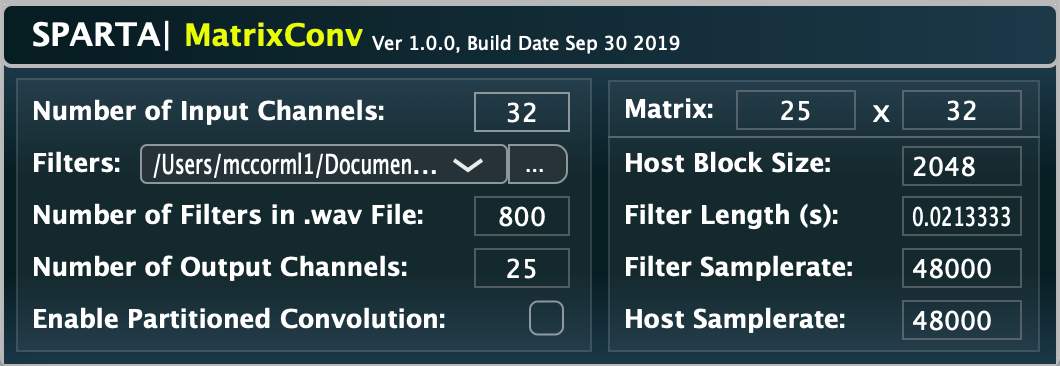
A simple matrix convolver with an (optional) partitioned-convolution mode. The matrix of filters should be concatenated for each output channel and loaded as a .wav file. You need only inform the plug-in of the number of input channels, and it will take care of the rest.

• Example 1, spatial reverberation: if you have a B-Format/Ambisonic room impulse response (RIR), you may convolve it with a monophonic input signal and the output will exhibit (much of) the spatial characteristics of the measured room. Simply load this Ambisonic RIR into the plug-in and set the number of input channels to 1. You may then decode the resulting Ambisonic output to your loudspeaker array (e.g. using SPARTA|AmbiDEC) or to headphones (e.g. using SPARTA|AmbiBIN). However, please note that the limitations of lower-order Ambisonics for signals (namely, colouration and poor spatial accuracy) will also be present with lower-order Ambisonic RIRs; at least, when applied in this manner. Consider referring to Example 3, for a more spatially accurate method of reproducing the spatial characteristics of rooms that are captured as B-Format/Ambisonic RIRs.
• Example 2, microphone array to Ambisonics encoding: if you have a matrix of filters to go from an Eigenmike (32 channel) recording to 4th order Ambisonics (25 channel), then the plugin requires a 25-channel wav file to be loaded, and the number of input channels to be set to 32. In this case: the first 32 filters will map the input to the first output channel, filters 33-64 will map the input to the second output channel, … , and the last 32 filters will map the input to the 25th output channel. An example of such an encoding matrix may be downloaded from here. Note that these example filters employ the ACN/N3D convention, Tikhonov regularisation, and 15dB of maximum gain amplification; using the Matlab scripts from here. This should be the same as SPARTA|Array2SH when it is set to the Eigenmike preset and default settings (except N3D not SN3D).
• Example 3, more advanced spatial reverberation: if you have a monophonic recording of a trumpet and you wish to reproduce it as if it were in your favourite concert hall, first measure a B-Format/Ambisonic room impulse response (RIR) of the hall, and then convert this Ambisonic RIR to your loudspeaker set-up using HO-SIRR. Then load the resulting rendered loudspeaker array RIR into the plug-in and set the number of input channels to 1. Note that you may prefer to use HO-SIRR (which is a parametric renderer), to convert your arbitrary order B-Format/Ambisonic IRs to arbitrary loudspeaker array IRs, as the resulting output will generally be much more spatially accurate when compared to linear (non-parametric) Ambisonic decoding; as described in Example 1. For the curious reader, an example of a 12point T-design loudspeaker array IR, made using a simulation [12] of the Vienna Musikverein concert hall, may be downloaded from here. To listen to the convolved output, either arrange 12 loudspeakers in a t-design for the playback (a bit cumbersome), or use the SPARTA|Binauraliser plug-in set to “T-Design (12)” and listen over headphones.
• Example 4, virtual monitoring of a multichannel setup: if you have a set of binaural head-related impulse responses (BRIRs) which correspond to the loudspeaker directions of a measured listening room, you may use this 2 x L matrix of filters to reproduce loudspeaker mixes (L-channels) over headphones. Simply concatenate the BRIRs for each input channel into a two channel wav file and load them into the plugin, then set the number of inputs to be the number of BRIRs/loudspeakers in the mix.

This plug-in was developed by Leo McCormack and Archontis Politis.

MultiConv#

A simple multi-channel convolver with an (optional) partitioned-convolution mode. The plugin will convolve each input channel with the respective filter up to the maximum of 64 channels/filters. The filters are loaded as a multi-channel .wav file.

Please note that this is not to be confused with the MatrixConv plug-in. For this plug-in, the number inputs = the number of filters = the number of outputs. i.e. no matrixing is applied.

• Example, headphone equalisation: post binauraliser/AmbiBIN etc., you may minimise the effect that your headphones have on the binaural output, by also convolving with (regularised) inverse filters. These filters may either be based on measurements of your own head and headphones, or you may download generic ones. For example, you can find equalisation filters for many commercially available headphones from here; which have been measured using a dummy head (more information can be found in [13]).

This plug-in was developed by Leo McCormack and Archontis Politis.

6DoFconv#

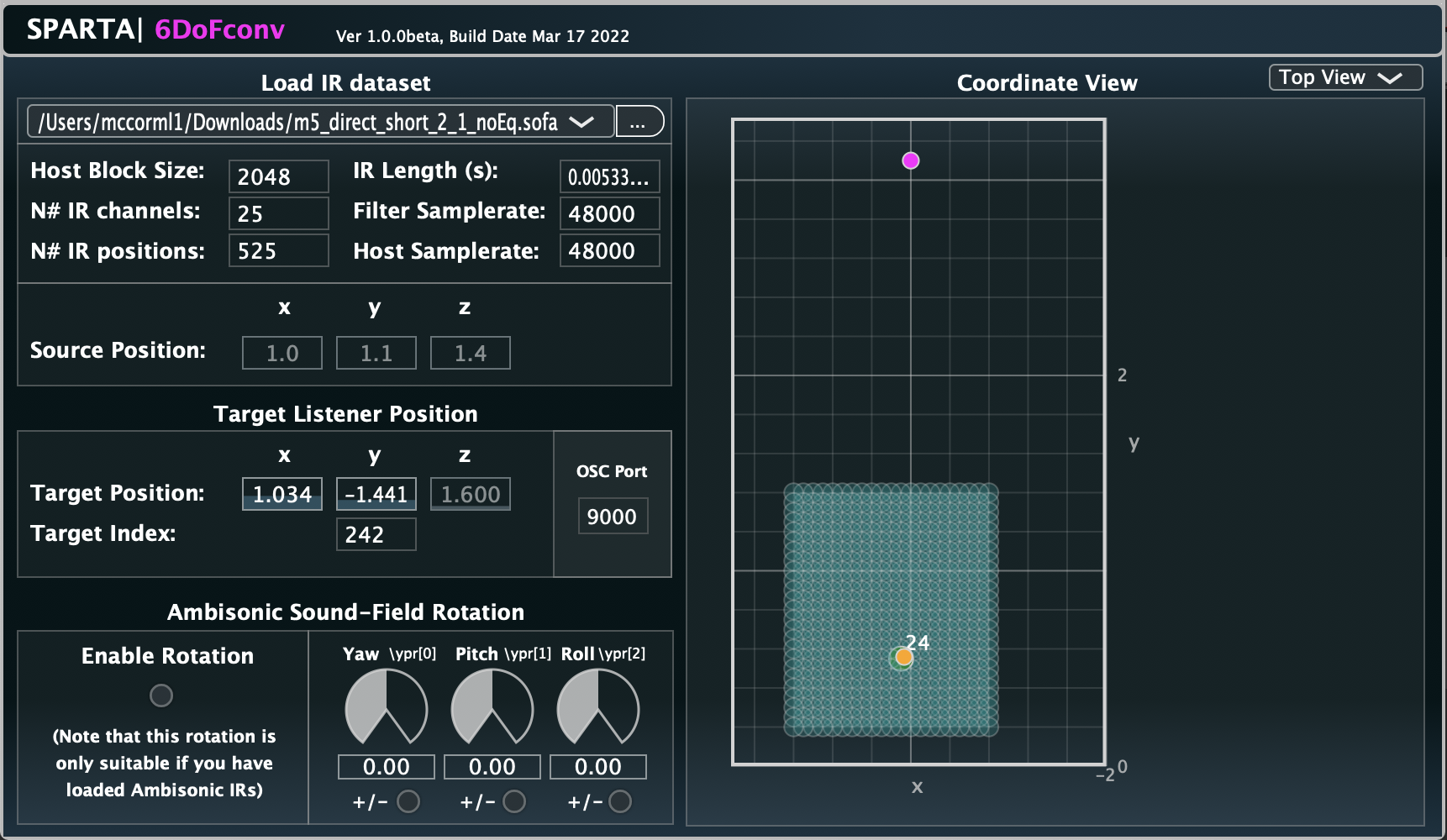
The 6DoFconv plug-in is related to this publication.

A time-varying partitioned convolution multi-channel convolver for SOFA files containing RIRs with multiple listener positions.

• Example, spatial reverberation: if you have a SOFA file of a dataset of B-format/Ambisonic spatial room impulse responses (SRIRs) with varying listener position, you may convolve one with a monophonic input signal, whereby the listener position (X, Y and Z coordinates) determines the SRIR selection. You may then decode the resulting Ambisonic output to your loudspeaker array (e.g. using SPARTA|AmbiDEC) or to headphones (e.g. using SPARTA|AmbiBIN). An example of SOFA files in a compatible format is the coupled room transition dataset (https://doi.org/10.5281/zenodo.4095493). For this, you may choose to use OSC signals in the format \xyzypr (denoting positional coordinates x, y, z and rotation yaw, pitch and roll) to control the listener position and orientation (enable rotation of the output).

This plug-in was developed by Rapolas Daugintis, Thomas McKenzie, Nils Meyer-Kahlen and Leo McCormack.

Panner#

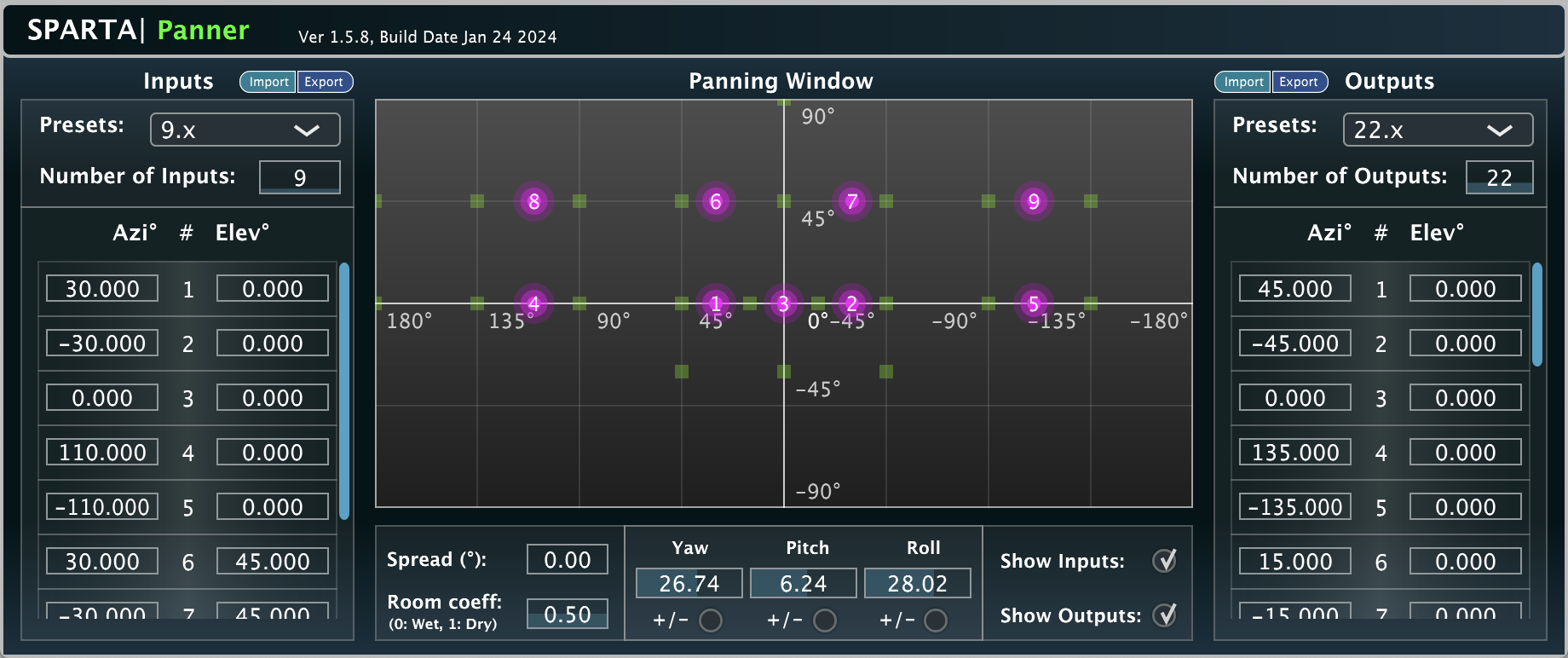
A frequency-dependent 3D panner based on the Vector-base Amplitude Panning (VBAP) method [4]. Presets for popular 2D and 3D formats are included for convenience; however, the directions for up to 64 channels can be independently controlled for both inputs and outputs; allowing, for example, 9.x input audio to be panned for a 22.2 setup. The panning is frequency-dependent to accommodate the method described in [5], which allows for more consistent loudness when sources are panned in-between the loudspeaker directions.

Set the “Room Coeff” parameter to 0 for standard power-normalisation, 0.5 for a listening room, and 1 for an anechoic chamber.

This plug-in was developed by Leo McCormack, Archontis Politis and Ville Pulkki.

PitchShifter#

A simple multi-channel pitch shifter (up to 64 channels) based on the phase vocoder approach.

PowerMap#

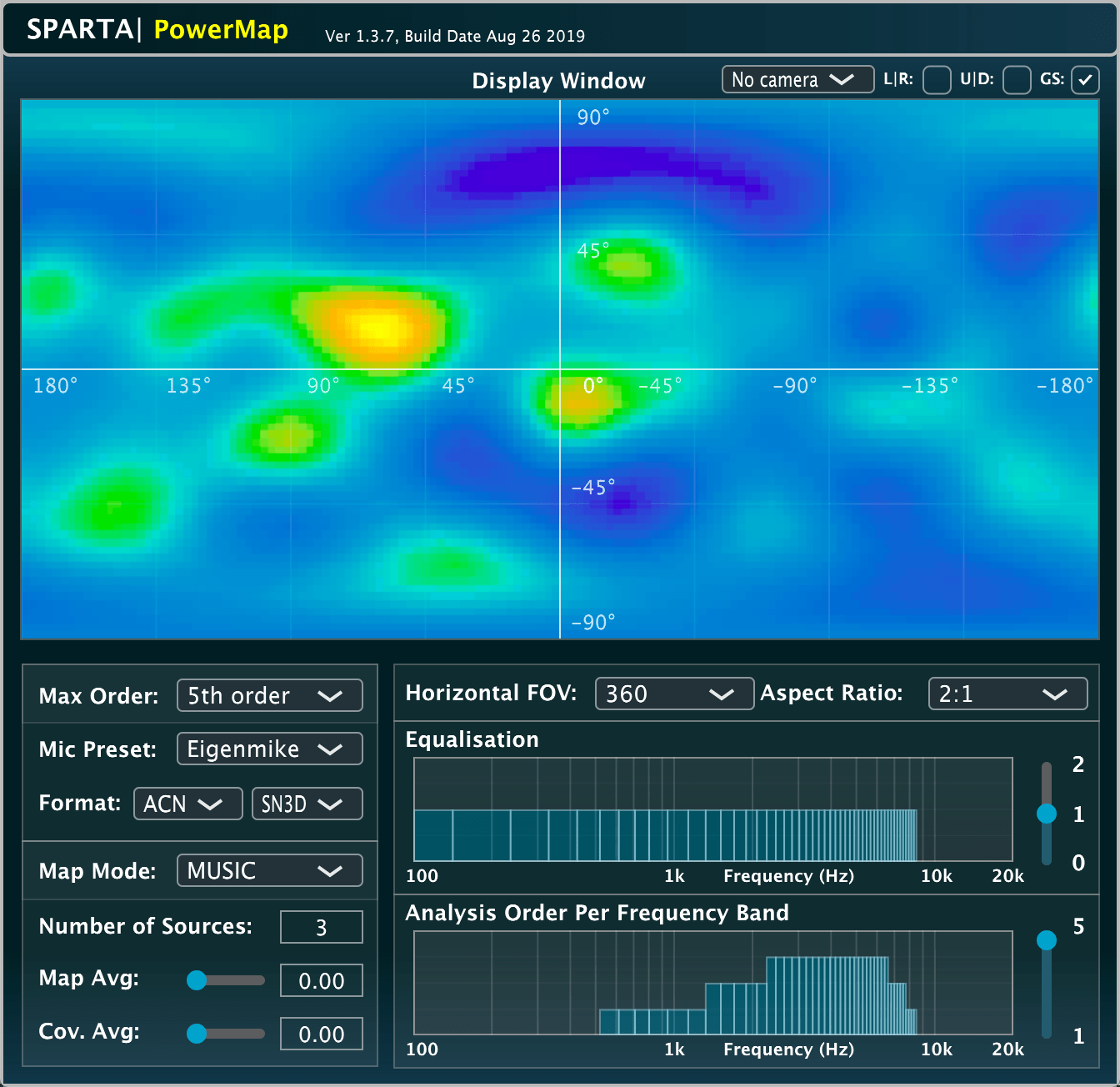
The PowerMap plug-in is a modified version of the plug-in described in this publication.

‘PowerMap’ is a plug-in that represents the relative sound energy, or the statistical likelihood of a source, arriving at the listening position from a particular direction, using a colour gradient; where yellow indicates high sound energy/likelihood and blue indicates low sound energy/likelihood. The plug-in integrates a variety of different approaches, including: standard Plane-Wave Decomposition (PWD) beamformer-based, Minimum-Variance Distortionless Response (MVDR) beamformer-based, Multiple Signal Classification (MUSIC) pseudo-spectrum-based, and the Cross-Pattern Coherence (CroPaC) algorithm [3]; all of which are written to operate on Ambisonic signals up to 10th order. Note that the analysis order per frequency band is entirely user definable, and presets for higher order microphone arrays have been included for convenience, which provide some rough starting values. The plug-in utilises a 812 point uniformly-distributed spherical grid, which is then interpolated into a 2D powermap using amplitude-normalised VBAP gains (i.e. triangular interpolation). The plug-in also allows the user to place real-time video footage behind the activity-map, in order to create a make-shift acoustic camera.

This plug-in was developed by Leo McCormack and Symeon Delikaris-Manias.

Rotator#

This plug-in applies a Ambisonic rotation matrix [6] to the input Ambisonic signals. The rotation angles can be controlled using a head tracker via OSC messages. Simply configure the headtracker to send a vector: ‘\ypr[3]’ to OSC port 9000 (default); where \ypr[0], \ypr[1], \ypr[2] are the yaw-pitch-roll angles, in degrees, respectively. The angles can also be flipped +/- in order to support a wider range of devices. The rotation order (yaw-pitch-roll (default) or roll-pitch-yaw) can also be specified. Alternatively, the rotation can be based on a Quaternion by sending vector: ‘\quaternion[4]'; where \quaternion[0], \quaternion[1], \quaternion[2], \quaternion[3], are the W, X, Y, Z parts of the Quaternion, respectively.

SLDoA#

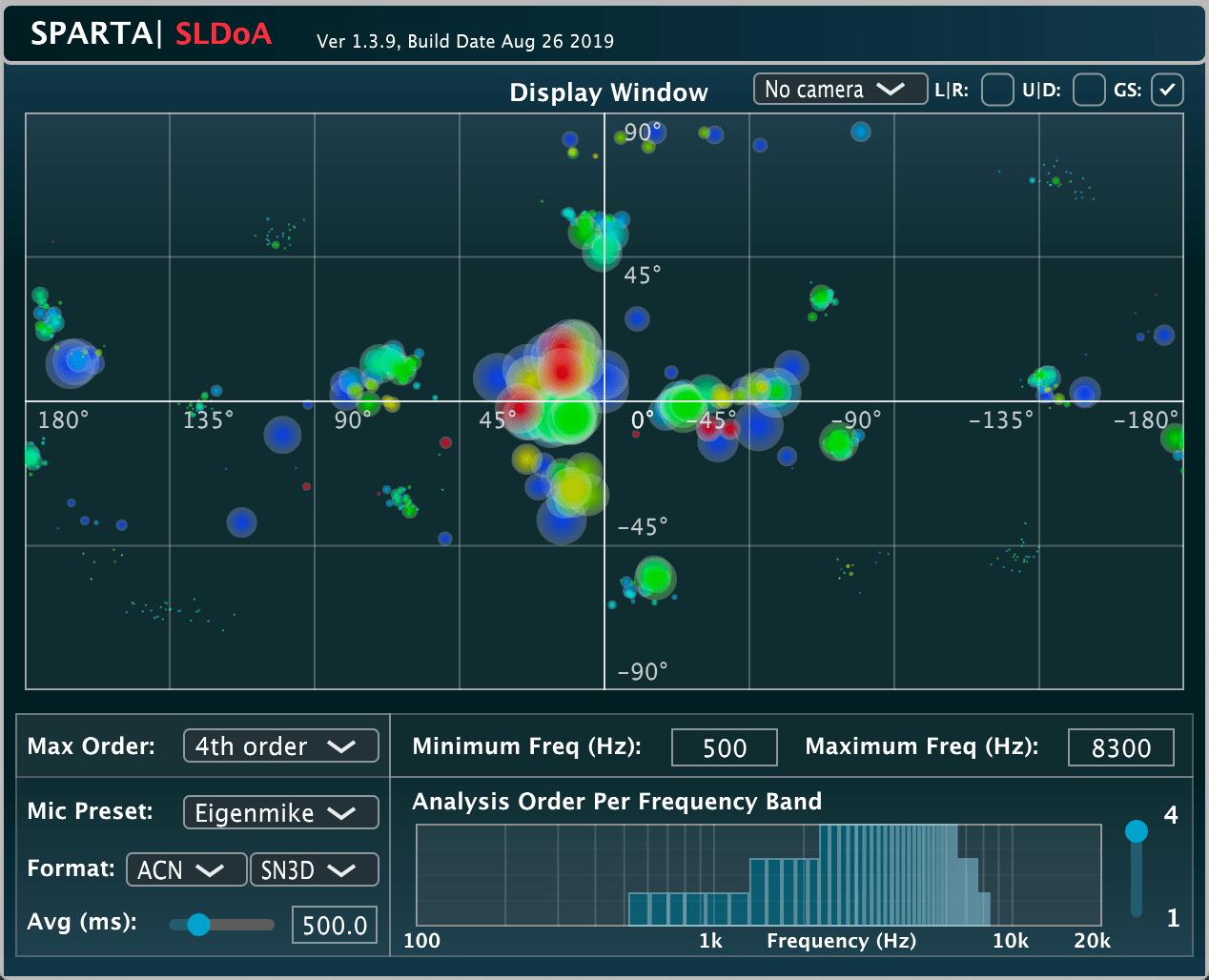
The SLDoA plug-in is related to these publications: Link1, Link2.

A spatially localised direction-of-arrival (DoA) estimator. The plug-in first uses VBAP beam patterns (for directions that are uniformly distributed on the surface of a sphere) to obtain spatially-biased zeroth and first-order signals, which are subsequently used for the active-intensity vector estimation; therefore, allowing for DoA estimation in several spatially-constrained sectors for each sub-band. The low frequency estimates are then depicted with blue icons, mid-frequencies with green, and high-frequencies with red. The size of the icon and its opacity correspond to the energy of the sector, which are normalised and scaled in ascending order for each frequency band. The plug-in employs two times as many sectors as the analysis order, with the exception of the first-order analysis, which uses the traditional active-intensity approach. The analysis order per frequency band is user definable, as is the frequency range at which to analyse. This approach to sound-field visualisation/DoA estimation represents a much more computationally efficient option, when compared to the algorithms that are integrated into the ‘Powermap’ plug-in, for instance. The plug-in also allows the user to place real-time video footage behind the activity-map, in order to create a make-shift acoustic camera.

This plug-in was developed by Leo McCormack and Symeon Delikaris-Manias.

Spreader#

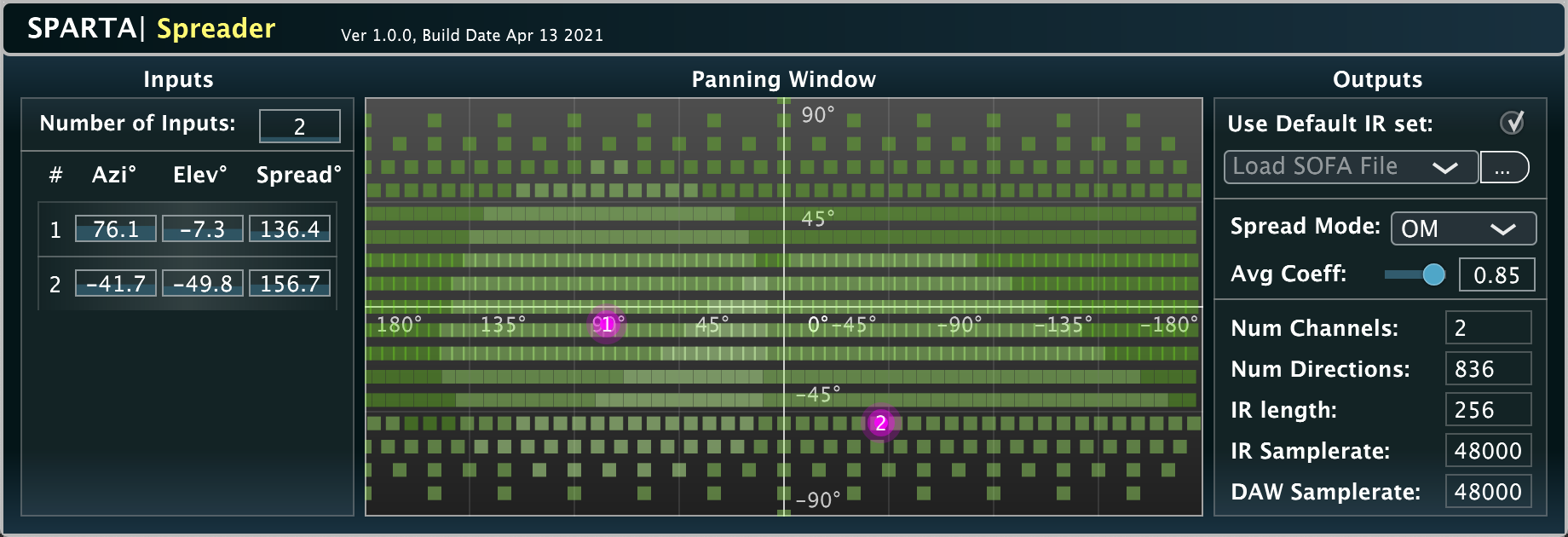
The Spreader plug-in is related to this publication.

This plugin uses an optimised framework for rendering spread sound sources over an arbitrary playback system, as described in [14]. In this particular implementation, the directional responses for the target system are loaded as impulse responses via the SOFA format (e.g., using HRIRs for binaural, or microphone array IRs for creating a synthetic recording). The algorithm is then tasked with mixing the input mono signals to produce the appropriate multi-channel signals (e.g. 2 for binaural playback, 4 or 32 for a synthetic tetrahedral microphone or Eigenmike array recording), such that the output signals create a diffuse, or rather: “incoherently spead” sound source. The solution is optimised to introduce decorrelated signal energy into the output only to the degree that is required to fulfill the target model. Therefore, the signal fidelity of the input signal is largely retained. The algorithm proposed in [14] is denoted as “OM” in this plug-in. For comparison, an unconstrained spatial covariance matching alternative is provided under the name “EVD”, which also fulfills the target model, but does so without the constraints for preserving signal fidelity. Additionally, a coherent spreading baseline (“BL”), which is commonly employed in the industry (e.g. game audio engines) is included, which can sound very unnatural when compared to the incoherent spreading alternatives.

This plug-in was developed by Leo McCormack and Archontis Politis.

About the developers#

• Leo McCormack: a postdoctoral researcher at Aalto University.
• Symeon Delikaris-Manias: post doctorate researcher at Aalto University, specialising in compact microphone array processing for DoA estimation and sound-field reproduction. His doctoral research included work on the Cross-Pattern Coherence (CroPaC) algorithm, which is a spatial post-filter optimised for high noise/reverberant environments.
• Archontis Politis: a professor at Tampere University, specialising in spatial sound recording and reproduction, acoustic scene analysis and microphone array processing.
• Ville Pulkki: Professor at Aalto University, known for VBAP, SIRR, DirAC and eccentric behaviour.
• Christoph Hold: a doctoral candidate at Aalto University.
• Michael McCrea: an audio R&D engineer.
• Sebastian Schlecht: a professor at Aalto University.
• Rapolas Daugintis: a doctoral candidate at Imperial College London.
• Thomas McKenzie: a lecturer in acoustics at the University of Edinburgh.
• Nils Meyer-Kahlen: a doctoral candidate at Aalto University.

License#

All of the plug-ins in the SPARTA suite may be used for academic, personal, and/or commercial use. The source code may also be used for commercial purposes, provided that the terms of the GPLv3 license are fulfilled. This requires that the original code and/or any derived works must also be open-sourced and made available under the same GPLv3 license, if it is to be used for commercial purposes.

References#

[1] Zotter, F., Frank, M. (2012). All-Round Ambisonic Panning and Decoding.
Journal of the Audio Engineering Society, 60(10), 807-820.

[2] Zotter, F., Pomberger, H., Noisternig, M. (2012). Energy-Preserving Ambisonic Decoding.
Acta Acustica United with Acustica, 98(1), 37-47.

[3] Delikaris-Manias, S., Pulkki, V. (2013). Cross pattern coherence algorithm for spatial filtering applications utilizing microphone arrays.
IEEE Transactions on Audio, Speech, and Language Processing, 21(11), 2356-2367.

[4] Pulkki, V. (1997). Virtual Sound Source Positioning Using Vector Base Amplitude Panning.
Journal of the Audio Engineering Society, 45(6), 456-466.

[5] Laitinen, M., Vilkamo, J., Jussila, K., Politis, A., Pulkki, V. (2014). Gain normalization in amplitude panning as a function of frequency and room reverberance.
55th International Conference of the AES. Helsinki, Finland.

[6] Ivanic, J., Ruedenberg, K. (1998). Rotation Matrices for Real Spherical Harmonics. Direct Determination by Recursion Page: Additions and Corrections.
Journal of Physical Chemistry A, 102(45), 9099-9100.

[7] Moreau, S., Daniel, J., Bertet, S. (2006). 3D sound field recording with higher order ambisonics-objective measurements and validation of spherical microphone.
in Audio Engineering Society Convention 120, Audio Engineering Society

[8] Politis, A., Gamper, H. (2017). Comparing Modelled And Measurement-Based Spherical Harmonic Encoding Filters For Spherical Microphone Arrays.
In IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA).

[9] Delikaris-Manias, S., McCormack, L., Huhtakallio, I., and Pulkki, V. (2018) Real-time underwater spatial audio: a feasibility study.
in Audio Engineering Society Convention 144, Audio Engineering Society.

[10] Zaunschirm, M., Schörkhuber, C., and Höldrich, R. (2018). Binaural rendering of Ambisonic signals by head-related impulse response time alignment and a diffuseness constraint.
The Journal of the Acoustical Society of America, 143(6), 3616-3627.

[11] Schörkhuber, C., Zaunschirm, M., and Höldrich, R. (2018). Binaural Rendering of Ambisonic Signals via Magnitude Least Squares.
In Proceedings of the DAGA (Vol. 44).

[12] Favrot, S. and Buchholz, J.M., (2019). LoRA: A loudspeaker-based room auralization system.
Acta Acustica united with Acustica, 96(2), pp.364-375.

[13] Bernschutz, B., (2013). A spherical far field HRIR/HRTF compilation of the Neumann KU 100.
In Proceedings of the 40th Italian (AIA) annual conference on acoustics and the 39th German annual conference on acoustics (DAGA) conference on acoustics (p. 29). AIA/DAGA.

[14] McCormack, L. Politis, A., and Pulkki, V., 2021, October. Rendering of source spread for arbitrary playback setups based on spatial covariance matching. In 2021 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA). IEEE.

[15] Spagnol, S., Tavazzi, E., and Avanzini, F. “Distance rendering and perception of nearby virtual sound sources with a near-field filter model.”
Applied Acoustics, vol. 115, pp. 61–73, Jan. 2017.

Other included plug-ins#

The SPARTA installer also includes:

• The COMPASS suite COMPASS →
• The HO-DirAC suite HO-DirAC →
• The HO-SIRR application HO-SIRR →
• The CroPaC-Binaural decoder CroPaC-Binaural →

Edit this page on GitHub